13.3. Working with Polygons
File:
Polygons.ml
From points and segments we move to more interesting two-dimensional objects — polygons.
To work with them, we will require a couple of auxiliary functions:
include Points
(* Some utility functions *)
let rec all_pairs ls = match ls with
| [] -> []
| _ :: [] -> []
| h1 :: h2 :: t -> (h1, h2) :: (all_pairs (h2 :: t))
let rec all_triples ls =
let (a, b) = (List.hd ls, List.hd @@ List.tl ls) in
let rec walk l = match l with
| x :: y :: [] -> [(x, y, a); (y, a, b)]
| x :: y :: z :: t -> (x, y, z) :: (walk (y :: z :: t))
| _ -> []
in
assert (List.length ls >= 3);
walk ls
(* Remove duplicates without sorting, via OCaml hashtable *)
let uniq lst =
let seen = Hashtbl.create (List.length lst) in
List.filter (fun x -> let tmp = not (Hashtbl.mem seen x) in
Hashtbl.replace seen x ();
tmp) lst
13.3.1. Encoding and rendering polygons
A polygon can be represented as a list of points:
type polygon = point list
We will use the following convention to interpret this list as a sequence of polygon vertices: as we “walk” along the list, the polygon is always on our left. OCaml’s representation of polygons uses the same convention.
It is more convenient to define polygons as list of integers (unless we specifically need coordinates expressed with decimals), hence the following auxiliary function:
let polygon_of_int_pairs l =
List.map (fun (x, y) ->
Point (float_of_int x, float_of_int y)) l
A very common operation is to shift polygon in a certain direction. This can be done as follows:
let shift_polygon (dx, dy) pol =
List.map (function Point (x, y) ->
Point (x +. dx, y +. dy)) pol
OCaml provides a special function draw_poly to render polygons, and we implement our machinery relying on it:
let draw_polygon ?color:(color = Graphics.black) p =
let open Graphics in
set_color color;
let ps_array = list_to_array @@ List.map point_to_orig p in
draw_poly ps_array;
set_color black
13.3.2. Some useful polygons
The following module defines a number of polygons with interesting properties:
module TestPolygons = struct
let triangle =
[(-50, 50); (200, 0); (200, 200)] |> polygon_of_int_pairs
let square = [(100, -100); (100, 100); (-100, 100); (-100, -100)] |> polygon_of_int_pairs
let convexPoly2 = [(100, -100); (200, 200); (0, 200); (0, 0)] |> polygon_of_int_pairs
let convexPoly3 = [(0, 0); (200, 0); (200, 200); (40, 100)] |> polygon_of_int_pairs
let simpleNonConvexPoly = [(0, 0); (200, 0);
(200, 200); (100, 50)] |> polygon_of_int_pairs
let nonConvexPoly5 = [(0, 0); (0, 200);
(200, 200); (-100, 300)] |>
polygon_of_int_pairs |>
shift_polygon (-50., -100.)
let bunnyEars = [(0, 0); (400, 0); (300, 200);
(200, 100); (100, 200)] |>
polygon_of_int_pairs |>
shift_polygon (-100., -50.)
let lShapedPolygon = [(0, 0); (200, 0); (200, 100);
(100, 100); (100, 300); (0, 300)]
|> polygon_of_int_pairs
|> shift_polygon (-150., -150.)
let kittyPolygon = [(0, 0); (500, 0); (500, 200);
(400, 100); (100, 100); (0, 200)]
|> polygon_of_int_pairs
|> shift_polygon (-250., -150.)
let simpleStarPolygon = [(290, 0); (100, 100); (0, 290);
(-100, 100); (-290, 0); (-100, -100);
(0, -290); (100, -100)] |> polygon_of_int_pairs
let weirdRectPolygon = [(0, 0); (200, 0); (200, 100); (100, 100);
(100, 200); (300, 200); (300, 300); (0, 300)]
|> polygon_of_int_pairs
|> shift_polygon (-150., -150.)
let sand4 = [(0, 0); (200, 0); (200, 100); (170, 100);
(150, 40); (130, 100); (0, 100)]
|> polygon_of_int_pairs
|> shift_polygon (-30., -30.)
let tHorror = [(100, 300); (200, 100); (300, 300);
(200, 300); (200, 400)]
|> polygon_of_int_pairs
|> shift_polygon (-250., -250.)
let chvatal_comb = [(500, 200); (455, 100); (400, 100);
(350, 200); (300, 100); (250, 100);
(200, 200); (150, 100); (100, 100);
(50, 200); (0, 0); (500, 0)]
|> polygon_of_int_pairs
|> shift_polygon (-200., -70.)
let chvatal_comb1 = [(500, 200); (420, 100); (400, 100);
(350, 200); (300, 100); (250, 100);
(200, 200); (150, 100); (100, 100);
(50, 200); (0, 70); (500, 70)]
|> polygon_of_int_pairs
|> shift_polygon (-200., -70.)
let shurikenPolygon = [(390, 0); (200, 50); (0, 290);
(50, 150); (-200, -100); (0, 0)]
|> polygon_of_int_pairs
|> shift_polygon (-80., -70.)
end
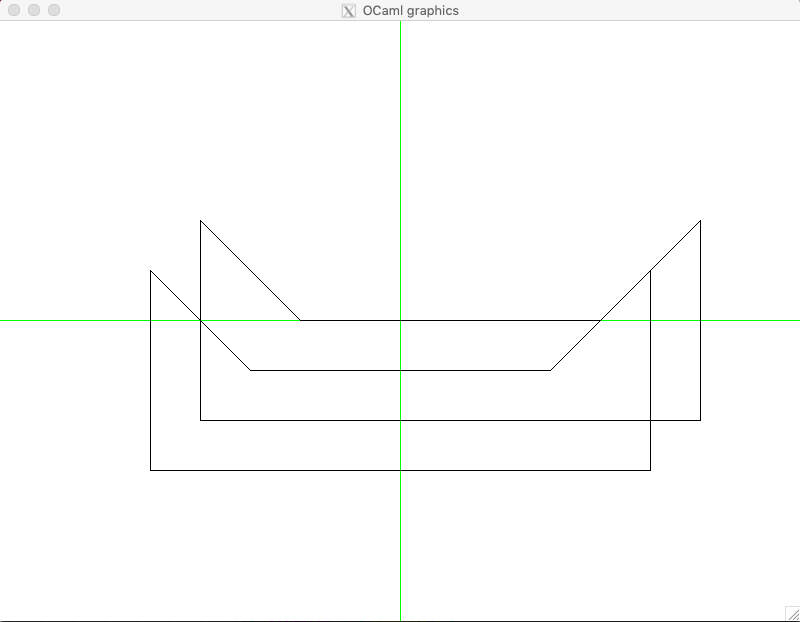
Let us render some of those:
utop # open Polygons;;
utop # open TestPolygons;;
utop # mk_screen ();;
utop # draw_polygon kittyPolygon;;
utop # let k1 = shift_polygon (50., 50.) kittyPolygon;;
utop # draw_polygon k1;;
13.3.3. Basic polygon manipulations
In addition to moving polygons, we can also resize and rotate polygons. The first operation is done by multiplying all vertices (as they were vectors) by the defined factor:
let resize_polygon k pol =
List.map (function Point (x, y) ->
Point (x *. k, y *. k)) pol
For rotation, we need to specify the center, relative to which the rotations is going to be performed. After that the conversion to polar coordinates and back does the trick:
let rotate_polygon pol p0 angle =
pol |>
List.map (fun p -> p -- p0) |>
List.map polar_of_cartesian |>
List.map (function Polar (r, phi) ->
Polar (r, phi +. angle)) |>
List.map cartesian_of_polar |>
List.map (fun p -> p ++ (get_x p0, get_y p0))
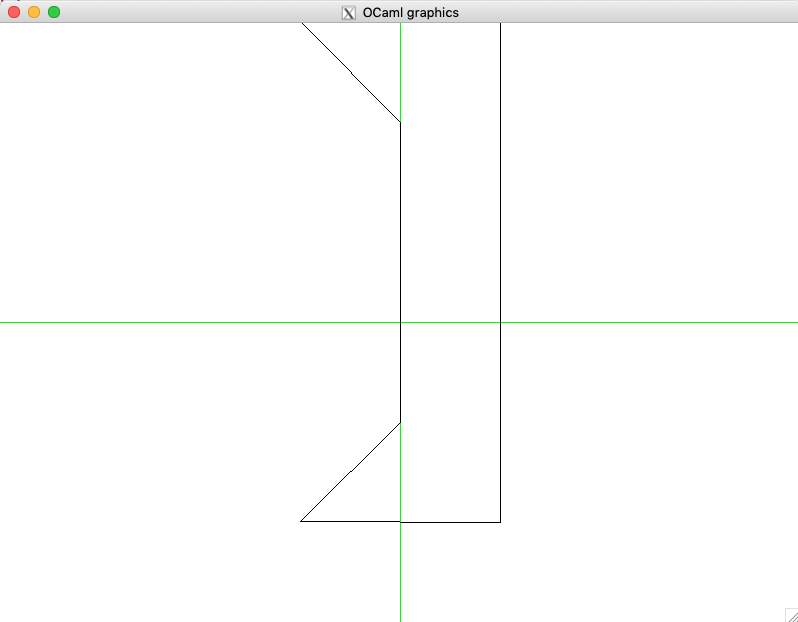
Here is an example of using thoe functions:
utop # let k2 = rotate_polygon k1 (Point (0., 0.)) (pi /. 2.);;
utop # clear_screen ();;
utop # draw_polygon k2;;
13.3.4. Queries about polygons
One of non-trivial properties of a polygon is convexity. A polygon is convex if any segment connecting points on its edges fully lies within the polygon. That is, checking convexity out of this definition is cumbersome, and there is a better way to do it, by relying one the machinery for determining directions. In essence, a polygon is convex if each three consecutive vertices in it do not form a right turn:
let is_convex pol =
all_triples pol |>
List.for_all (fun (p1, p2, p3) -> direction p1 p2 p3 <= 0)
Another property to check of two fixed polygons, is whether they intersect, which would mean a collision. This can be checked in a time proportional to the product of the sizes of the two polygons, via the following functions, checking pair-wise intersection of all of the edges:
let edges pol =
if pol = [] then []
else
let es = all_pairs pol in
let lst = List.rev pol |> List.hd in
let e = (lst, List.hd pol) in
e :: es
let polygons_touch_or_intersect pol1 pol2 =
let es1 = edges pol1 in
let es2 = edges pol2 in
List.exists (fun e1 ->
List.exists (fun e2 ->
segments_intersect e1 e2) es2) es1
13.3.5. Intermezzo: rays and intersections
The procedure above only checks for intersection of edges, but what is one polygon is fully within another polygon? How can we determine that? To answer this question, we would need to be able to determine whether a certain point is within a given polygon. But for this we would need to make a small detour and talk about another geometric construction: rays.
Ray is similar to a segment, but only has one endpoint, spreading to the infinity in a certain direction. This is why we represent rays by its origin and an angle in radians (encoded as float), determining the direction in which it spreads:
type ray = point * float
let draw_ray ?color:(color = Graphics.black) r =
let (p, phi) = r in
let open Graphics in
let q = p ++ (2000. *. (cos phi), 2000. *. (sin phi)) in
draw_segment ~color (p, q)
Given a ray \(R = (p, \phi)\) and a point \(p\) that belongs to the line of the ray, we can determine whether \(p\) is on \(r\) by means of the following function:
let point_on_ray ray p =
let (q, phi) = ray in
(* Ray's direction *)
let r = Point (cos phi, sin phi) in
let u = dot_product (p -- q) r in
u >=~ 0.
Notice that here we encode all points of \(R\) via the equation \(q + u r\), where \(r\) is a “directional” vector of the ray and \(0 \leq u\). We then solve the vector equation \(p = q + u r\), by multiplying both parts by \(r\) via scalar product, and also noticing that \(r \cdot r = 1\). Finally, we check if \(u \geq 0\), to make sure that \(p\) is not lying “behind” the ray.
Now, we can find an intersection of a ray and a segment, in a way similar to how that was done in Section Points, Segments and their Properties:
let ray_segment_intersection ray seg =
let (p, p') = seg in
let (q, phi) = ray in
(* Segment's direction *)
let s = Point (get_x p' -. get_x p, get_y p' -. get_y p) in
(* Ray's direction *)
let r = Point (cos phi, sin phi) in
(* Ray and Segment are parallel *)
if cross_product s r =~= 0. then
(* Ray and Segment are collinear *)
if cross_product (p -- q) r =~= 0.
then if point_on_ray ray p then Some p
else if point_on_ray ray p' then Some p'
else None
else None
else begin
(* Point on segment *)
let t = (cross_product (q -- p) r) /. (cross_product s r) in
(* Point on ray *)
let u = (cross_product (p -- q) s) /. (cross_product r s) in
if u >=~ 0. && t >=~ 0. && t <=~ 1.
then
let Point (sx, sy) = s in
let z = p ++ (sx *. t, sy *. t) in
Some z
else
None
end
Specifically, if the ray and the segment are collinear than we can try to find if one of the end points of the segment is on the ray.
Otherwise, if they are not collinear, we express them both in the vector form
and solve two equations, wrt. the scalar parameters t and u. Finally, we
check that u and t are in the allowed ranges, and use one of them to
calculate the intersection point.
13.3.6. Point within an polygon
A simple way to determine whether a point is within a polygon if to draw a ray
(in an arbitrary direction) from it and count how many times it intersect the
edges of the polygon. If this number is odd, the point is within the polygon,
otherwise it is outside. This is done by the procedure point_within_polygon
defined below, along with several auxiliary functions:
(* Get neightbors of a vertex *)
let get_vertex_neighbours pol v =
assert (List.mem v pol);
let arr = Array.of_list pol in
let n = Array.length arr in
assert (Array.length arr >= 3);
if v = arr.(0) then (arr.(n - 1), arr.(1))
else if v = arr.(n - 1) then (arr.(n - 2), arr.(0))
else let rec walk i =
if i = n - 1 then (arr.(n - 2), arr.(0))
else if v = arr.(i)
then (arr.(i - 1), arr.(i + 1))
else walk (i + 1)
in walk 1
(* Get neightbors of a vertex *)
let neighbours_on_different_sides ray pol p =
if not (List.mem p pol) then true
else
let (a, b) = get_vertex_neighbours pol p in
let (r, d) = ray in
let s = r ++ (cos d, sin d) in
let dir1 = direction r s a in
let dir2 = direction r s b in
dir1 <> dir2
To avoid conrer cases, it makes sense to cast the ray from p in a way that
so it would not be collinear with any of the edges and not pass through any
vertices. For this, we will need the following function:
let choose_ray_angle pol p =
let Point (xp, yp) = p in
let edge_angles =
edges pol |>
List.map (fun (Point (x1, y1), Point (x2, y2)) ->
let dx = x2 -. x1 in
let dy = y2 -. y1 in
atan2 dy dx) in
let vertex_angles =
pol |> List.map (fun (Point (x1,y1)) ->
let dy = y1 -. yp in
let dx = x1 -. xp in
atan2 dy dx) in
let n = 2 * (List.length pol) + 1 in
let candidate_angles =
iota (n + 1) |>
List.map (fun i ->
(float_of_int i) *. pi /. (float_of_int n)) in
let phi = List.find (fun c -> List.for_all
(fun a -> not (a =~= c))
edge_angles &&
List.for_all
(fun a -> not (a =~= c))
vertex_angles) candidate_angles in
phi
Now, we can determine whether the point is within the polygon:
(* Point within a polygon *)
let point_within_polygon pol p =
let ray = (p, (choose_ray_angle pol p)) in
let es = edges pol in
if List.mem p pol ||
List.exists (fun e -> point_on_segment e p) es then true
else
begin
let n =
edges pol |>
List.map (fun e -> ray_segment_intersection ray e) |>
List.filter (fun r -> r <> None) |>
List.map (fun r -> get_exn r) |>
(* Intersecting a vertex *)
uniq |>
(* Touching vertices *)
List.filter (neighbours_on_different_sides ray pol) |>
(* Compute length *)
List.length
in
n mod 2 = 1
end
A few corner cases have to be taken into the account:
A ray may contain the entire edge of the polygon.
A ray may “touch” a sharp vertex — in this case this intersection should not count. However, if a ray “passes” through a vertex (as opposed to touching it), this should count as an intersection.
The case (a) does not happen, as we have chosen the ray to be not collinear with any of th edges.
In the case (b) case, duplicating intersections need to be removed
first, hence the use of uniq. The configuration can be detected by
checking whether two adjacent edges to the node suspected in
“touching” lie on the single side or on two opposite sides of the ray.
Only the second case (detected via neighbours_on_different_sides)
needs to be accounted.
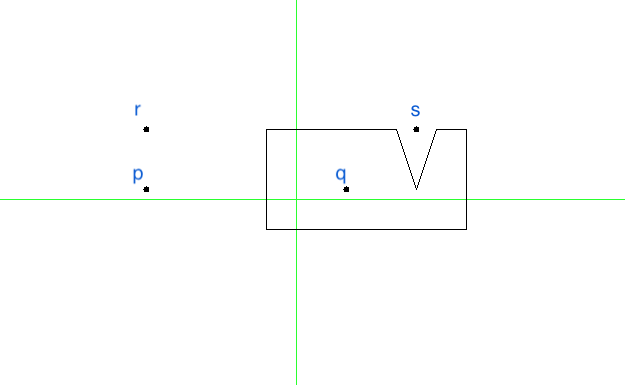
We can test our procedure on the following polygon:
utop # let pol = TestPolygons.sand4;;
utop # let p = Point (-150., 10.);;
utop # let q = Point (50., 10.);;
utop # let r = Point (-150., 70.);;
utop # let s = Point (120., 70.);;
utop # point_within_polygon pol p;;
- : bool = false
utop # point_within_polygon pol q;;
- : bool = true
utop # point_within_polygon pol r;;
- : bool = false
utop # point_within_polygon pol s;;
- : bool = false