5. Final Project: Vroomba Programming
In these difficult times, it is particularly important to keep our living spaces clean and tidy. To help with this task, the researchers from NUS Faculty of Engineering have designed a new advanced cleaning robot called Vroomba 1. In this project, you will have to develop a series of algorithms for navigating a Vroomba robot across arbitrary spaces so it could clean them. The catch is: you will have to strive to minimise the number of “moves” the Vroomba needs to make it to do its job.
A room is represented by a two-dimensional rectilinear polygon with
all coordinates being integer values. Vroomba occupies one square
1x1, and its position is formally defined to be the bottom left
corner of this square. Vroomba instantly cleans the space in the
square it is located. In addition to that, its mechanical brushes can
clean the eight squares adjacent to its current position.
Unfortunately, the manipulators cannot spread through the walls or
“wrap” around the corners.

Your goal in this task is to compute for a Vroomba robot that starts the job at
the position (0, 0), as good as possible route to clean the entire area of
room. For example, consider a room defined as the polygon with coordinates (0,
0); (6, 0); (6, 1); (8, 1); (8, 2); (6, 2); (6, 3); (0, 3) and shown on the
image below:
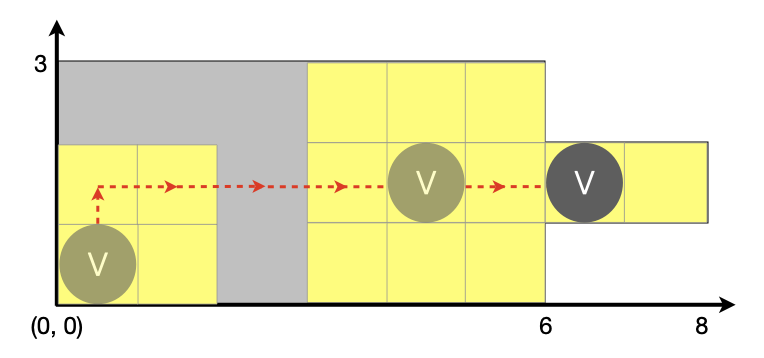
In order to clean the entire room the Vroomba positioned initially in the
coordinate (0, 0) can move by following the route defined by the string of
moves WDDDDDD (all characters are capital), where W makes Vroomba move
one square up, D moves it right, S is “down”, and A is “left”. The
figure above shows an initial (0, 0), some intermediate (4, 1), and the
final (6, 1) positions of the Vroomba following this route. Notice that
there is was no need for the robot to step to any other squares, as it brushes
cleaned the remaining parts of the room, as it is following the rout.
The suggested route is a valid one for this room, as it (a) does not force the Vroomba to go outside the room boundaries, and (b) by following it, the Vroomba will have cleaned all the squares in the room. Indeed, for more complex rooms the routes are going to be longer and potentially use all four move commands in some sequence.
When tackling this project, you should strive to find, for a given arbitrary room, a valid Vroomba route that is as short as possible (the length of a route is the length of the corresponding string). While it might be difficult to find the most optimal (i.e., the shortest) route, please, do your best to come up with a procedure that finds a “reasonably” good solution, for instance, it does not make the Vroomba to move into every single square of the room, but relies on the range of its brushes instead. Even the best solution might require amount of back-tracking, forcing the Vroomba to step on the same square more than once. While your procedure is allowed to be computationally expensive (and you should explain the sources of its complexity in comments in the code), it should terminate in a reasonable time (within 20 seconds) for the ten rooms from the provided test file.
Document via comments in your code:
High-level overview of your implementation design. How did you define basic data structures, what were the algorithmic decisions you’ve taken?
What were your Vroomba solver strategies, interesting polygon generation patterns, or game part enhancements? How do you estimate the complexity of your solver as a function of the size of a room (number of
1x1squares in it)?What you considered important properties of your implementation? How did you test them?
How the implementation effort has been split, and what were your personal contributions? Did you make use of the suggested split?
Any discoveries, anecdotes, and gotchas, elaborating on your experience with this project.
- 1
Any relation to the existing products or trademarks is accidental.