12.2. Graphs as Linked Data Structures

• File Graphs.ml

Let us consider a more efficient implementation of graphs as a linked heap-based data structure. The implementation features some redundancy, in order to provide an efficient access to the nodes of a graph as well as their adjacent neighbours. The implementation will rely on data structures developed previously: hash-tables and sets, represented via BSTs.

We start by defining the data type for nodes:

module LinkedGraphs = struct

  (*************************************************)
  (*                     Nodes                     *)
  (*************************************************)

  type 'a node = {
    id : int;
    value : 'a ref;
    next : int list ref;
    prev : int list ref
  }

  let get_value n = !(n.value)
  let get_next n = !(n.next)
  let get_prev n = !(n.prev)

  let add_prev node src =
    let prev' = get_prev node |>
                List.filter (fun n -> n <> src) in
    node.prev := src :: prev'

  let add_next node dst =
    let next' = get_next node |>
                List.filter (fun n -> n <> dst) in
    node.next := dst :: next'

  (* More types and functions are coming here *)

end

Each node stores its identifier (an integer), a payload value, as well as lists of “previous” and “next” nodes in the graph (initially empty).

We now define a graph as follows:

(*************************************************)
(*           Auxiliary definitions               *)
(*************************************************)

open BST
open BetterHashTable

module Set = BinarySearchTree
module NodeTable =
  ResizableListBasedHashTable(struct type t = int end)
module EdgeTable =
  ResizableListBasedHashTable(struct type t = int * int end)

type 'a set = 'a Set.tree

(*************************************************)
(*                Working with Graphs            *)
(*************************************************)

type ('a, 'b) graph = {
  next_node_id : int ref;
  nodes : int set;
  node_map : (int * 'a node) NodeTable.hash_table;

  edges : (int * int) set;
  edge_labels : ((int * int) * 'b) EdgeTable.hash_table
}

That is, a graph contains:

• a counter next_node_id used to allocate identifiers for newly added nodes;

• a set (represented via BST) nodes of all node identifies;

• node_map for mapping node identifiers to node objects;

• a set of edges (edges);

• a hash map of edge labels (edge_labels).

The graph structure defined just above allows to access the set of predecessors/successors of a node in a constant time, as opposed to linear one with the list-based representation. Consider the following utility functions:

(* Graph size *)
let v_size g = !(g.next_node_id)
let e_size g = BinarySearchTree.get_size g.edges
let get_nodes g = Set.elements g.nodes

(* Refer to the node in the graph *)
let get_node g i = get_exn @@ NodeTable.get g.node_map i

let get_succ g n =
  let node = get_node g n in
  get_next node

let get_prev g n =
  let node = get_node g n in
  get_prev node

let node_in_graph g n =
  let nodes = g.nodes in
  Set.search nodes n <> None

let edge_in_graph g src dst =
  let nodes = g.edges in
  Set.search nodes (src, dst) <> None

As the linked graph structure combines five conceptually “overlapping” components, it needs to be maintained with a lot of care, in order not to introduce any discrepancies in the representations.

Creating new empty graph is easy:

let mk_graph _ = {
  next_node_id = ref 0;
  nodes = Set.mk_tree ();
  node_map = NodeTable.mk_new_table 10;
  edges = Set.mk_tree ();
  edge_labels = EdgeTable.mk_new_table 10
}

Adding a node requires allocating a new identifier for it, registering it in both the set of node identifiers, and the node map:

let add_node g v =
  let new_id = !(g.next_node_id) in
  g.next_node_id := !(g.next_node_id) + 1;
  let node = {
    id = new_id;
    value = ref v;
    next = ref [];
    prev = ref [];
  } in
  (* Register node *)
  let _ = Set.insert g.nodes new_id in
  (* Register node payload *)
  NodeTable.insert g.node_map new_id node

Adding an edge requires modifying the corresponding node instances to account for new predecessors and successors:

let add_edge g src dst =
  assert (node_in_graph g src && node_in_graph g src);
  (* Register edge *)
  let _ = Set.insert g.edges (src, dst) in
  (* Add information to individual nodes *)
  let src_node = get_exn @@ NodeTable.get g.node_map src in
  let dst_node = get_exn @@ NodeTable.get g.node_map dst in
  add_prev dst_node src;
  add_next src_node dst

We can also set a new label to an edge (src, dst) as follows:

let set_edge_label g src dst l =
  assert (node_in_graph g src && node_in_graph g src);
  assert (edge_in_graph g src dst);
  (* Register label *)
  EdgeTable.insert g.edge_labels (src, dst) l

12.2.1. Switching between graph representations

As we already have reading/writing implemented for AL-based graphs, let us implement conversion between them and linked representations. The following function, for instance, converts a simple AL-based graph (with arbitrary node payloads) to a linked representation:

let from_simple_adjacency_graph (ag : ('a, 'b) AdjacencyGraphs.graph) =
  let g = mk_graph () in

  (* Add nodes *)
  for i = 0 to ag.size - 1 do
    let v = snd @@ List.find (fun (n, _) -> n = i) !(ag.node_payloads) in
    add_node g v;
  done;

  (* Add edges *)
  for i = 0 to ag.size - 1 do
    ag.adj.(i) |>
    List.map (fun n -> (i, n)) |>
    List.iter (fun (src, dst) -> add_edge g src dst)
  done;

  (* Add edge labels *)
  List.iter (fun ((src, dst), l) -> set_edge_label g src dst l)
    !(ag.edge_labels);

  g

Conversely, the following function obtains an adjacency graph from a linked representation:

let to_adjacency_graph g =
  let size = v_size g in
  let ag = AdjacencyGraphs.mk_graph size in

  (* Set node payloads *)
  Set.elements g.nodes |>
  List.iter (fun n ->
      let node = get_exn @@ NodeTable.get g.node_map n in
      AdjacencyGraphs.set_payload ag n (get_value node));

  (* Add edges *)
  let edges = Set.elements g.edges in
  List.iter (fun (src, dst) -> AdjacencyGraphs.add_edge ag src dst) edges;

  (* Add edges labels *)
  List.iter (fun (s, d) ->
      match EdgeTable.get g.edge_labels (s, d) with
      | None -> ()
      | Some l -> AdjacencyGraphs.set_edge_label ag s d l) edges;
  ag

We can now put those functions to use for getting linked graphs immediate from the strings and files:

let parse_linked_int_graph ls =
  AdjacencyGraphs.adjacency_int_graph_of_strings ls |>
  from_simple_adjacency_graph

let read_simple_linked_graph_from_file filename =
  let ag = AdjacencyGraphs.read_simple_graph_shape_from_file filename in
  from_simple_adjacency_graph ag

12.2.2. Testing graph operations

One advantage of AL-based representation is that it makes it considerably easier to test graphs for certain properties. For instance, the following function checks that two AL-represented graphs have the same topology assuming the exact correspondence of the nodes (i.e., the same sets of node identifiers, and edges between them):

let same_shape (ag1 : ('a, 'b) AdjacencyGraphs.graph)
    (ag2 : ('a, 'b) AdjacencyGraphs.graph) =
  assert (ag1.size = ag2.size);
  let n = ag1.size in
  let comp x y = if x < y
    then - 1
    else if x > y
    then 1 else 0 in
  for i = 0 to n - 1 do
    let adj1 = ag1.adj.(i) |> List.sort comp in
    let adj2 = ag1.adj.(i) |> List.sort comp in
    assert (adj1 = adj2)
  done;
  true

We can use it to check that out AL-to-linked-and-back conversion preserves the graph shape. Take the following graph:

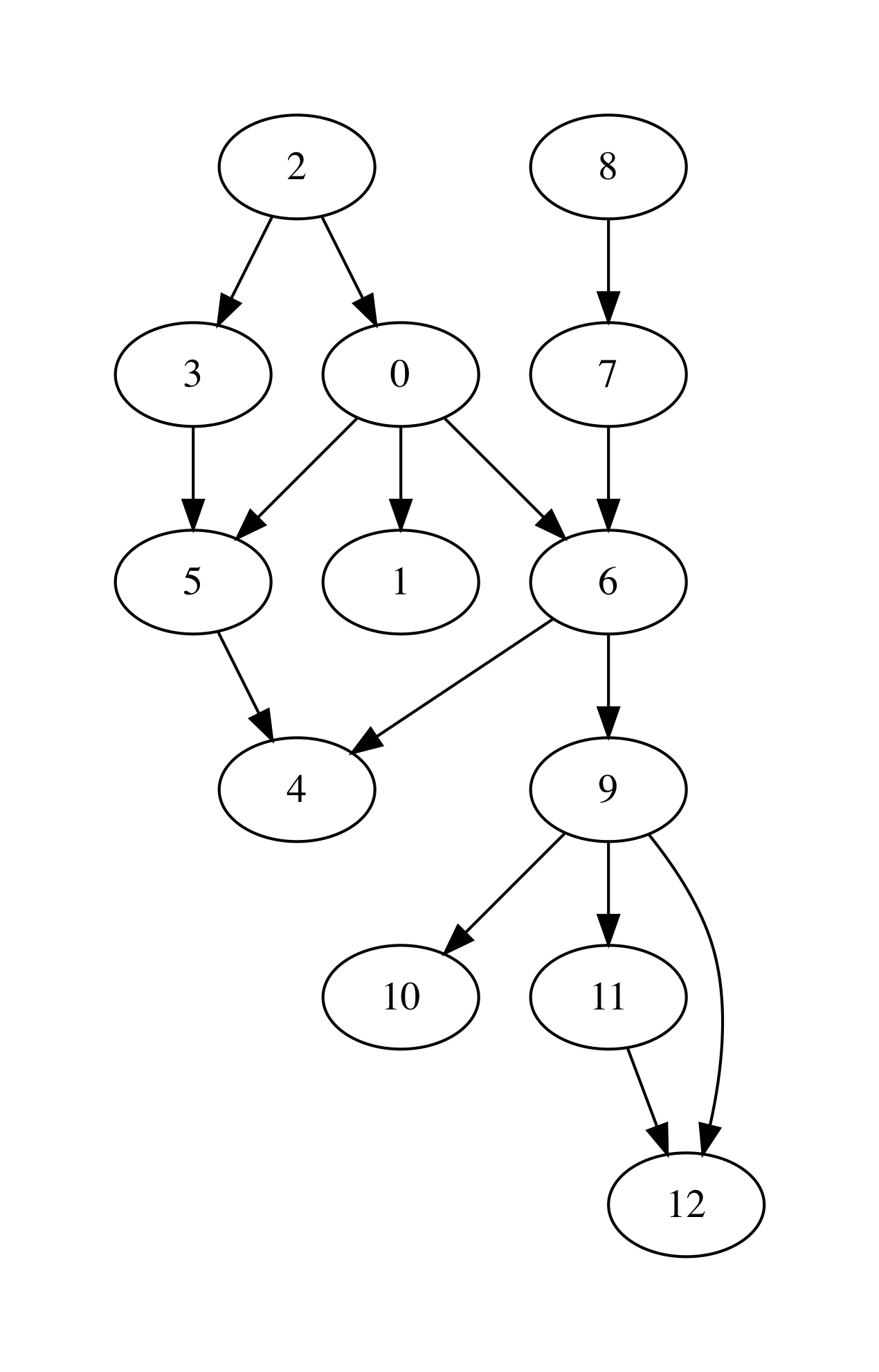
let medium_graph_shape =
  ["13";
   "0 1";
   "0 6";
   "0 5";
   "2 0";
   "2 3";
   "3 5";
   "5 4";
   "6 4";
   "7 6";
   "8 7";
   "6 9";
   "9 10";
   "9 11";
   "9 12";
   "11 12"]

We can now make sure that the following test succeeds:

let%test _ =
  let ag = AdjacencyGraphs.adjacency_int_graph_of_strings medium_graph_shape in
  let g = LinkedGraphs.from_simple_adjacency_graph ag in
  let ag' = LinkedGraphs.to_adjacency_graph g in
  same_shape ag ag'

We can also try out the conversion machinery for the sake of producing nice GraphViz images:

utop # let g = LinkedGraphs.parse_linked_int_graph medium_graph_shape;;
utop # let ag = LinkedGraphs.to_adjacency_graph g;;
utop # graphviz_no_payload ag "medium.dot";;

Now, by running from the terminal:

dot -Tpdf medium.dot -o medium.pdf

we obtain the following image: